问题
选择题
已知O、N、P在△ABC所在的平面内,且|
|
答案
因为|
|=|OA
|=|OB
|,所以0到顶点A,B,C的距离相等,所以O为△ABC的外心.OC
由
•PA
=PB
•PB
=PC
•PC
,得(PA
-PA
)•PC
=0,即PB
•AC
=0,所以AC⊥PB.PB
同理可证AB⊥PC,所以P为△ABC的垂心.
若
+NA
+NB
=NC
,则0
+NA
=-NB
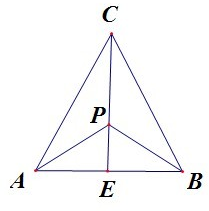
,取AB的中点E,则NC
+NA
=2NB
=NE
所以2|NE|=|CN|,CN
所以N是△ABC的重心.
故选B.
