问题
问答题
某消费者的效用函数和预算约束分别为U=
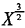Y和3X+4Y=100，而另一消费者的效用函数为U=X6Y4+1.5lnX+lnY，预算约束也是3X+4Y=100。求：
(1)他们各自的最优商品购买数量。
(2)最优商品购买量是否相同这与两条无差异曲线不能相交矛盾吗
答案
参考答案：某消费者的效用函数和预算约束分别为U=[*]Y和3X+4Y=100，而另一消费者的效用函数为U=X6Y4+1.5lnX+lnY，预算约束也是3X+4Y=100。求：
(1)他们各自的最优商品购买数量。
(2)最优商品购买量是否相同这与两条无差异曲线不能相交矛盾吗
解析：[解] (1)对于U=[*]Y，有[*][*]。由预算约束3X+4Y=100，可知PX =3，PY=4；[*]即为[*]
[*]
第一消费者最优商品购买为X=20，Y=10；
对于U=X6Y4+1.5lnX+lnY有：[*]由预算约束可知 PX=3，PY=4；[*]即为[*]
[*]
第二消费者的最优商品购买也是X=20，Y=10。
(2)两个人的最优商品购买是相同的，这样两条无差异曲线就经过同样的点，似乎与两条无差异曲线不能相交矛盾。其实，是不矛盾的。因为两个消费者都有自己的无差异曲线图，在各自的无差异曲线图中，两条无差异曲线是不相交的；但上述两个消费者的两条无差异曲线在不同的无差异曲线图中，不存在相交不相交的问题，只不过它们分别与同样的预算线3X+4Y=100相切，切点也相同，都是点(20，10)。值得注意的是，点(20，10)在两个人看来，所代表的效用是不一样的。