问题
单项选择题
某人工湖,形状如下图所示,图中AE与CD相互平行,AB与BC相互垂直,AC与CD相互垂直,AB长为400米,BC长为300米,CD长为475米,DE长为625米,现要沿着湖边植树,要求在A、B、C、D、E处都植一棵树,问至少应植树多少棵()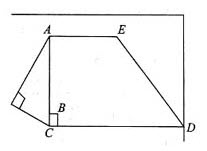
A.72
B.74
C.76
D.78
答案
参考答案:C
解析:
这是一道几何和植树的综合题目。植树问题的核心在于找出植树的总长和间距。本题的解题步骤如下:①根据已知条件算出AE的长度,则人工湖的周长就求出来了;②确定每棵树之间的间距;③根据封闭路线植树公式求解。解题过程如下:①根据勾股定理可知AC=500米,且(CD-AE)2=ED2-AC2,代入题目已知条件解出AE=100米。②根据“要求在A、B、C、D、E处都植一棵树”,可推知植树的间距应为400、300、475、625和100的约数,题目要求植树最少,那么间距就应该最大,则最大间距为人工湖5个边的最大公约数即25。根据封闭路线植树公式,“棵树=全长÷间距”,可知至少应植树(400+300+475+625+100)÷25=76棵。故选C。
