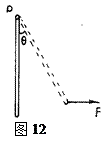
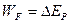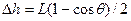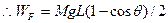如图12所示粗细均匀的木棒长为L,质量为M ,可绕固定转动轴O自由转动,现用水平力F作用于木棒的下端将木棒从竖直位置缓慢拉起,并转过θ角度,则在拉起的过程中,拉力F做的功为多少?
某同学解法为:
木棒与竖直位置成θ时,木棒所受的力矩平衡 Mg Lsinθ/2=" F" Lcosθ,
得到F=Mgtgθ/2
从竖直位置缓慢拉起的过程中, 拉力F从0变化到Mgtgθ/2,
拉力F的平均值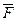 =Mgtgθ/4
=Mgtgθ/4
拉力作用点在力F方向上的位移是 S="L" sinθ
根据W="FS " 解得 :拉力F 做的功:WF=" Mg" L sinθtgθ/4
所以在拉起的过程中,拉力F做的功为WF="Mg" L sinθtgθ/4 ,
你认为他的解法是否正确?若正确,请说明理由;若错误,也请说明理由,并且解出正确的结果。
不正确
沿水平方向F力不是均匀地增加,所以不能用力的算术平均值来计算此力所做的功。
正确解法: 根据能量守恒,力F所做的功等于木棒势能增加量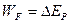

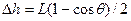
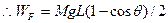
不正确
沿水平方向F力不是均匀地增加,所以不能用力的算术平均值来计算此力所做的功。
正确解法: 根据能量守恒,力F所做的功等于木棒势能增加量