问题
问答题
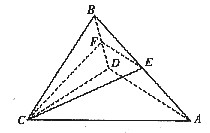
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD上的中点。
(1)求证:直线EF∥平面ACD;
(2)求证:平面EFC⊥平面BCD。
答案
参考答案:(1)∵点E,F分别是AB,BD的中点,
∴EF是AABD的中位线,
∴EF∥AD。
∵EF[*]平面ACD,AD[*]平面ACD,
∴直线EF∥平面ACD。
(2)∵AD⊥BD,EF∥AD,
∴EF⊥BD。
∵CB=CD,点F是BD的中点,
∴CF⊥BD。
又EF∩CF=F.
∴BD⊥平面EFC。
[*]
∴平面EFC⊥平面BCD。