问题
计算题
一个连同装备总质量为M=100kg的宇航员，在距离飞船x=45m处与飞船处于相对静止状态，宇航员背着装有质量为m0=0.5 kg氧气的贮气筒。筒上装有可以使氧气以v=50 m/s的速度喷出的喷嘴，宇航员必须向着返回飞船的相反方向放出氧气，才能回到飞船，同时又必须保留一部分氧气供途中呼吸用，宇航员的耗氧率为Q=2.5×10-4 kg/s，不考虑喷出氧气对设备及宇航员总质量的影响，则：
(1)瞬时喷出多少氧气，宇航员才能安全返回飞船？
(2)为了使总耗氧量最低，应一次喷出多少氧气？返回时间又是多少？
答案
解：(1)结合题目中的第(1)、第(2)两问不难看出，第(1)问所求的喷出氧气的质量m应有一个范围，若m太小，宇航员获得的速度也小，虽贮气筒中剩余的氧气较多，但由于返回飞船所用的时间太长，将无法满足他途中呼吸所用，若m太大，宇航员获得的速度虽然大了，而筒中氧气太少，也无法满足其呼吸作用，所以m对应的最小和最大两个临界值都应是氧气恰好用完的情况，设瞬间喷气m kg时，宇航员恰能安全返回，根据动量守恒定律可得：
mv=MV ①
宇航员匀速返回的时间为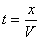
②
贮气筒中氧气的总质量：m0≥m+Qt ③
代入数据可得0.05 kg≤m≤0.45 kg
(2)当总耗氧量最低时，设宇航员安全返回时，共消耗氧气△m，则△m=m+Qt ④
由①②④可得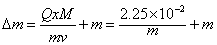
当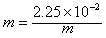
即m=0.15 kg时，△m有极小值，故总耗氧量最低时，应一次喷出0.15 kg的氧气
将m=0.15 kg代入①②两式可解得返回时间：t=600 s