如图9所示，竖直平面内放一直角杆，杆的水平部分粗糙，竖直部分光滑，两部分各套有质量分别为mA="2.0" kg和mB="1.0" kg的小球A和B，A球与水平杆间动摩擦因数μ=0.20，A、B间用不可伸长的轻绳相连，图示位置处OA="1.5" m，OB="2.0" m.g取10 m/s2.
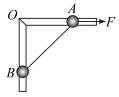
图9
（1）若用水平力F1沿杆向右拉A，使A由图示位置向右极缓慢地移动0.5 m，则该过程中拉力F1做了多少功？
（2）若用水平力F2沿杆向右拉A，使B以1 m/s的速度匀速上升，则在B经过图示位置上升0.5 m的过程中，拉力F2做了多少功？
（1）0.8 J (2)6.8 J
（1）A、B小球和细绳整体竖直方向处于平衡，A受到水平杆的弹力为
N=（mA+mB）g ①
则A受到的摩擦力为f=μ（mA+mB）g ②
由几何关系，sB="0.5" m ③
由能量关系，拉力F1做功为：
W1=fsA+mBgsB ④
得：W1="0.8" J ⑤
(2)设细绳与竖直方向的夹角为θ，因绳不可伸长，所以vBcosθ=vAsinθ ⑥
则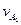
=vBcotθ1=
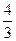m/s， ⑦
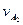=vBcotθ2=
m/s ⑧
设拉力F2做功为W2，对系统由能量关系得W2-fsA-mBgsB=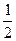
mAvA22-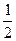mAvA21 ⑨
代入数据解得W2="6.8" J ⑩
