问题
解答题
已知f(x)=
(1)化简f(x) (2)若x是第三象限角,且sin(x+
|
答案
(1)f(x)=
=sin(π-x)cos(2π-x)tan(-x+3π) -tan(-x-π)sin(-
-x)9π 2
=sinx.sinxcosxtan(-x) -tanxcosx
(2)因为sin(x+
)=-cosx=3π 2
所以cosx=-1 5
,1 5
因为x是第三象限角,所以sinx=-
=-1-cos2x
=-1-(-
)21 5
.所以f(x)=-2 6 5
.2 6 5

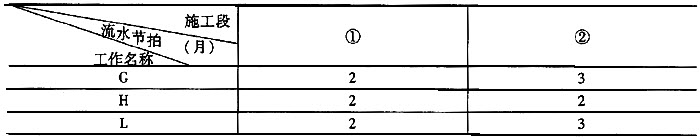 问题4:G、H、L3项工作流水施工的工期为多少此时工程总工期能否满足原竣工日期的要求为什么
问题4:G、H、L3项工作流水施工的工期为多少此时工程总工期能否满足原竣工日期的要求为什么