问题
问答题
设α1，α2，α3，α4，β为四维列向量，A=[α1，α2，α3，α4]，已知Ax=β的通解为
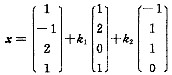，其中
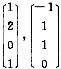为对应齐次方程组的基础解系，k1，k2为任意常数．令B=[α1，α2，α3]，试求By=β的通解．
答案
参考答案：[详解] 由题设知：r(A)=2，且有β=α1-α2+2α3+α4，
α1+2α2+0α3+α4=0，
-α1+α2+α3+0α4=0．
于是有 α3=α1-α2，α4=-α1-2α2，β=2α1-5α2+0α3．
可见α1，α2线性无关，r(B)=2，且[*]为By=β的特解，
又由α1-α2-α3=0知[*]为By=0的非零解，可作为基础解系，
故By=β的通解为[*]，其中k为任意常数．
解析：
[分析]： 本题是线性方程组求解的逆问题，已知非齐次线性方程组Ax=β的一个特解，相当于告之β可由A的列向量组线性表示的关系式，而已知齐次线性方程组Ax=0的一个解，相当于告之A的列向量之间的一个线性组合．反过来，求By=β的通解，只须找出β用B的列向量线性表示的关系式(确定相应特解)以及B的列向量之间的线性组合(确定相应基础解系)即可．
[评注] 类似本题的线性方程组求解的逆问题，可以更全面地考查相关知识的掌握情况，在复习过程中应引起考生重视．