如图所示，竖直平面内放一直角杆AOB，杆的水平部分粗糙，动摩擦

问题问答题

如图所示，竖直平面内放一直角杆AOB，杆的水平部分粗糙，动摩擦因数μ=0.20，杆的竖直部分光滑，两部分各套有质量分别为2.0kg和1.0kg的小球A和B，A、B间用细绳相连，初始位置OA=1.5m，OB=2.0m，g取10m/s²，则

（1）若用水平拉力F₁沿杆向右缓慢拉A，使之移动0.5m，该过程中A受到的摩擦力多大？拉力F₁做功多少？

（2）若小球A、B都有一定的初速度，A在水平拉力F₂的作用下，使B由初始位置以1.0m/s的速度匀速上升0.5m，此过程中拉力F₂做功多少？

答案

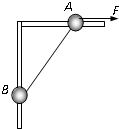
（1）先对AB整体受力分析，如图所示．

A、B小球和细绳整体竖直方向处于平衡，A受到的弹力为：

N=（m_A+m_B）g

则A受到的摩擦力为F_f=μ（m_A+m_B）g

代入数字得：F_f=6N

由几何关系，s_B=0.5m

由能量关系，拉力F₁做功为：W₁=F_fs+m_Bgs_B；

代入数字得：W₁=20 J

（2）设细绳与竖直方向的夹角为θ，因细绳不可伸长，两物体沿绳子方向的分速度大小相等，所以有

v_Bcosθ=v_Asinθ

则：A的初速度vA1=vBcotθ1=

m/s

末速度 vA2=vBcotθ2=

m/s

设拉力F₂做功为W₂，对系统，由能量关系得：W2-FfsB-mBgsB=

2A2

2A1

代入数据得W₂=6.8 J

答：

（1）A受到的摩擦力为6N，力F₁作功为20J．

（2）力F₂作功为6.8J．