问题
计算题
如图所示,竖直面内的正方形导线框ABCD、abcd的边长均为l、总电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场. 开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l. 现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动. 不计摩擦和空气阻力,求:
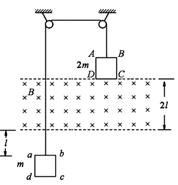
(1)系统匀速运动的速度大小.
(2)两线框从开始运动至等高的过程中所产生的总焦耳热.
(3)线框abcd通过磁场的时间.
答案
(1) 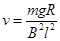 (2)
(2)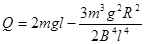 (3)
(3)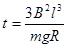
题目分析:解:(1)设两线框刚匀速运动的速度为v、此时轻绳上的张力为T,则对ABCD有: 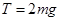 ①
①
对abcd有: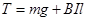 ②
②
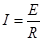 ③
③
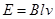 ④
④
则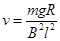 ⑤
⑤
(2)设两线框从开始运动至等高的过程中所产生的焦耳热为Q,当左、右两线框分别向上、向下运动2l的距离时,两线框等高,对这一过程,由能量守恒有:
由能量守恒定律有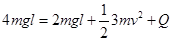 ⑥
⑥
解⑤⑥得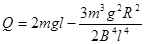
(3)线框abcd通过磁场时以速度v匀速运动,设线框abcd通过磁场的时间为t则
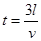 ⑦
⑦
解⑤⑦得: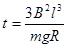
点评:导体杆在上升过程中,安培力随着速度增加而变大,当匀速时正好处于平衡状态.由法拉第电磁感应定律与闭合电路殴姆定律可求出速度大小.
