问题
计算题
如图所示,在倾角θ=30°,相距L=1m的光滑轨道上端连有一电阻R=9Ω,整个轨道处于垂直轨道方向的磁感应强度B=1T的匀强磁场中,现在轨道上由静止释放一质量m=100g,电阻r=lΩ的金属棒,当棒下滑s=5m时恰好达到最大速度,不计导轨电阻.
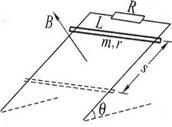
求:
(1)棒下滑的最大速度.
(2) 棒下滑的速度为3m/s时棒的加速度大小为多少
(3) 电阻R在这个过程中产生的热量.
答案
(1)5m/s(2)a=2m/s2(3)1.125J
题目分析:(1)滑棒在下滑过程中速度最大时,加速度a为零,此时有:mgsinθ=B2L2vm/(R+r),由此可解得最大速度vm=mgsinθ(R+r)/B2L2=5m/s
(2)a=2m/s2
(3)由功能关系可求出滑棒在下滑过程中产生的热量Q=mgssinθ-mvm2/2=1.25J.
QR=0.9Q=1.125J
点评:解决本题的关键会根据牛顿第二定律求加速度,以及结合运动学能够分析出金属棒的运动情况,当a=0时,速度达到最大.

