问题
填空题
| 给出下列命题: ①函数y=sin(
②函数y=cos(2x+
③对于任意实数x,有f(-x)=-f(x),g(-x)=g(x),且x>0时,f′(x)>0,g′(x)>0,则x<0时,f′(x)>g′(x); ④若对∀x∈R,函数f(x)满足f(x+2)=-f(x),则4是该函数的一个周期. 其中真命题的个数为______. |
答案
对于①,因为y=sin(
+x)=-cosx,是偶函数;故①正确;3π 2
对于②,因为函数y=cos(2x+
)图象的对称轴方程为2x+π 4
=kπ,因为x=π 4
不满足对称轴方程;故②不正确;π 8
对于③;由于对于任意实数x,有f(-x)=-f(x),g(-x)=g(x),
所以f(x)为奇函数;g(x)为偶函数;
又因为x>0时,f′(x)>0,g′(x)>0,
所以f(x)在(0,+∞)上单调递增;g(x)在(0,+∞)上单调递增;
所以f(x)在(-∞,0)上单调递增;g(x)在(-∞,0)上单调递减;
所以x<0时,f′(x)>0;g′(x)<0;
则x<0时,f′(x)>g′(x);故③正确;
对于④,对∀x∈R,函数f(x)满足f(x+2)=-f(x),所以f(x+4)=-f(x+2),所以f(x+4)=f(x)
所以4是该函数的一个周期.故④正确;
所以①③④为真命题,
故答案为:3

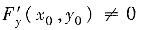 是F(x,y)=0在点(x0,y0)某邻域能确定一个连续函数y=y(x),它满足y0=y(x0),并有连续的导数的______条件.
是F(x,y)=0在点(x0,y0)某邻域能确定一个连续函数y=y(x),它满足y0=y(x0),并有连续的导数的______条件.