问题
单项选择题
设F(x，y)在点(x0，y0)某邻域有连续的偏导数，F(x0，y0)=0，则
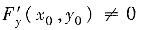是F(x，y)=0在点(x0，y0)某邻域能确定一个连续函数y=y(x)，它满足y0=y(x0)，并有连续的导数的______条件.
A．必要非充分
B．充分非必要
C．充分且必要
D．既不充分又不必要
答案
参考答案：B
解析：由隐函数
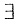定理知，在题设条件下，
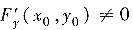是方程F(x，y)=0在点(x0，y0)某邻域能确定一个连续函数y=y(x)，满足y0=y(x0)并有连续导数的充分条件，但不是必要条件. 如F(x，y)=x3-xy，F(0，0) =0，
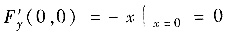，但F(x，y)=0确定函数y=x2(满足y(0)=0).
因此选B.