问题
计算题
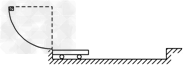
如图所示，一质量为M的小车静止在光滑水平面上，水平面左右两侧均为固定的竖直墙壁，左侧与一光滑固定的1/4圆弧相连，半径R＝0.8 m，圆弧底端切线水平且与车的上表面平齐，将一质量为m的小滑块(可视为质点)从圆弧顶端由静止释放后滑下，滑块与车的上表面间的动摩擦因数μ＝0.3，已知M＝3m，小车所在的水平面足够长(即滑块与小车的速度相同前小车不会与墙壁相碰)，且小车每次与墙壁的碰撞都不损失机械能(取g＝10 m/s2)．求：
(1)小车第一次与墙壁相碰前的速度．
(2)要保证滑块始终不从车上掉下来，车长至少为多少？
答案
解：(1)滑块下滑到圆弧底端时速度设为v0，第一次与墙壁碰撞前共同速度设为v1
根据机械能守恒：mgR＝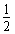
mv02 ①
滑块在车上滑动过程中系统动量守恒：mv0＝(m＋M)v1 ②
又由题意知：M＝3m ③
联立①②③并代入数据解得：v1＝1 m/s
即小车第一次与墙壁相碰撞前的速度为1 m/s
(2)设小车第一次与墙壁相碰撞前滑块在车上相对滑过的距离设为l1，根据能量守恒有：
μmgl1＝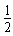
mv02－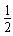
(m＋M)v12 ④
小车第一次与墙壁碰后反向向左运动，二者共同速度运动时的速度设为v2
在此过程中，车与滑块系统动量守恒：Mv1－mv1＝(M＋m)v2 ⑤
设此过程中滑块相对小车向右滑动的距离为l2
根据能量守恒有：μmgl2＝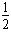
(m＋M)v12－
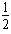(m＋M)v22 ⑥
经研究发现，此后小车与墙壁两侧分别碰撞后，滑块与小车系统损失的机械能逐次减少，相对滑过的距离也减小，而且相对滑动的方向依次改变，故车
长至少应为l＝l1＋l2 ⑦
联立④⑤⑥⑦并代入数据解得：l＝2.5 m