问题
填空题
直线y=kx（k＞o）与曲线y=x2围成图形的面积为
|
答案
先根据题意画出图形，得到积分上限为k，积分下限为0
直线y=kx与曲线y=x2所围图形的面积S=∫0k（kx-x2）dx
而∫0k（kx-x2）dx=（
kx2-1 2
x3）|0k=1 3
k3-1 2
k3=1 3
k3=1 6 4 3
∴解得k=2
故答案为：2．
搜题请搜索小程序“爱下问搜题”
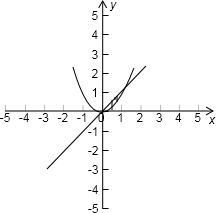
直线y=kx（k＞o）与曲线y=x2围成图形的面积为
|
先根据题意画出图形，得到积分上限为k，积分下限为0
直线y=kx与曲线y=x2所围图形的面积S=∫0k（kx-x2）dx
而∫0k（kx-x2）dx=（
kx2-1 2
x3）|0k=1 3
k3-1 2
k3=1 3
k3=1 6 4 3
∴解得k=2
故答案为：2．