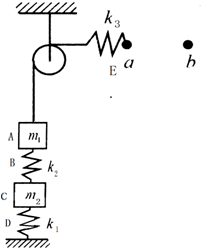
在如图所示的装置中,物体A和C的质量分别为m1、m2,弹簧D、B、E的劲度系数分别为k1、k2、k3,不计弹簧和细绳的质量,不计滑轮的摩擦.当弹簧E处在水平位置且未发生形变时,其右端点位于a位置.将弹簧E的右端点沿水平方向缓慢地从a位置拉到b位置时,弹簧E的拉力大小恰好等于A的重力.求:
(1)当弹簧E处在水平位置且未发生形变时,弹簧D的形变量.
(2)在弹簧E的右端点从a位置拉到b位置的过程中,物体A上升的高度是多少?a、b间的距离是多大?
(1)当弹簧E未发生形变时弹簧B、D都处于压缩状态,设压缩量分别为xB、xD.对于物体A和C、弹簧B整体,根据平衡条件和胡克定律有
对于物体A和C、弹簧B整体,k1xD=(m1+m2)g
解得弹簧D的形变量为xD=(m1+m2)g k1
对于物体A,k2xB=m1g
(2)当弹簧E的右端点拉到b位置时,因弹簧E的拉力大小恰好等于A的重力,说明此时弹簧E处于伸长状态,且伸长量xE=m1g k3
此时弹簧B恢复原长,弹簧D的压缩量变为xD′=m2g k1
所以物体A上升的高度为h=xD-xD′+xB
解得h=m1g(
+1 k1
)1 k2
ab间的距离为ab=h+xE
ab=m1g(
+1 k1
+1 k2
)1 k3
答:(1)弹簧D的形变量xD=
.(m1+m2)g k1
(2)物体A上升的高度是h=m1g(
+1 k1
),a、b间的距离是ab=m1g(1 k2
+1 k1
+1 k2
).1 k3
