问题
填空题
抛物线y=-x2+4x-3及其在点A(1,0)和点B(3,0)处的切线所围成图形的面积为_______.
答案
由y′=-2x+4和在点A,B处切线的斜率分别为2和-2,
则两直线方程分别为y=2x-2和y=-2x+6.
由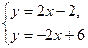 得C(2,2).
得C(2,2).
所以S=S△ABC-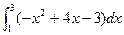 =
=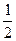 ×2×2-(-
×2×2-(- x3+2x2-3x)
x3+2x2-3x)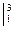 =2-
=2-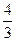 =
=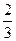 .
.
抛物线y=-x2+4x-3及其在点A(1,0)和点B(3,0)处的切线所围成图形的面积为_______.
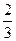
由y′=-2x+4和在点A,B处切线的斜率分别为2和-2,
则两直线方程分别为y=2x-2和y=-2x+6.
由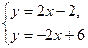 得C(2,2).
得C(2,2).
所以S=S△ABC-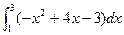 =
=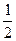 ×2×2-(-
×2×2-(- x3+2x2-3x)
x3+2x2-3x)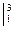 =2-
=2-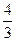 =
=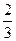 .
.