问题
解答题
直线y=kx将抛物线y=x-x2与x轴所围的图形分为面积相等的两部分,求k的值及直线方程.
答案
直线方程为y=(1-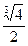 )x..
)x..
研究平面图形的面积的一般步骤是:(1)画草图;(2)解方程组,求出交点坐标;(3)确定被积函数及上、下限;(4)进行计算.
解:由 (0<k<1).
(0<k<1).
由题设得 ,
,
即 .
.
∴(1-k)3= .
.
∴k=1-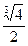 .
.
∴直线方程为y=(1-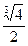 )x.
)x.
直线y=kx将抛物线y=x-x2与x轴所围的图形分为面积相等的两部分,求k的值及直线方程.
直线方程为y=(1-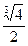 )x..
)x..
研究平面图形的面积的一般步骤是:(1)画草图;(2)解方程组,求出交点坐标;(3)确定被积函数及上、下限;(4)进行计算.
解:由 (0<k<1).
(0<k<1).
由题设得 ,
,
即 .
.
∴(1-k)3= .
.
∴k=1-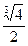 .
.
∴直线方程为y=(1-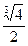 )x.
)x.