问题
解答题
已知函数f(x)=-x3+ax2-4(a∈R)，f′(x)是f(x)的导函数，
（Ⅰ）当a=2时，对于任意的m∈[-1，1]，n∈[-1，1]，求f(m)+f′(n)的最小值；
（Ⅱ）若存在x0∈(0，+∞)，使f(x0)＞0，求a的取值范围。
答案
解：（1）由题意知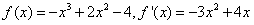
，
令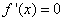
得x=0或
，
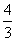当x在[-1，1]上变化时，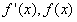
随x的变化情况如下表：
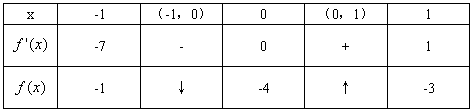
∴对于m∈[-1，1]，f(m)的最小值为f(0)=-4，
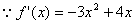的对称轴为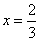
，且抛物线开口向下，
∴对于n∈[-1，1]，f′(n)的最小值为
，
∴f(m)+f′(n)的最小值为-11。
（2）
，
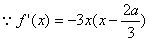①若a≤0，当x＞0时，f′(x)＜0，
∴f(x)在[0，+∞)上单调递减，
又f(0)=-4，则当x＞0时，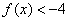
，
∴当a≤0时，不存在x0＞0，使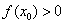
；
②若a＞0，则当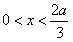
时，f′(x)＞0，
当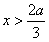
时，f′(x)＜0，
从而f(x)在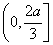
上单调递增，在
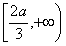上单调递减，
∴当x∈(0，+∞)时，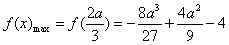
，
根据题意，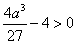
，即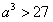
，解得a＞3；
综上，a的取值范围是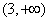
。
