问题
计算题
如图所示，空间存在竖直向上方向的匀强电场，E=2.0×102N/C，水平方向存在向外的匀强磁场，B=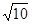
T，在A处有一个质量为0.3Kg的小球，所带电量为q=﹢2.0×10-2C。用长为L=6m的不可伸长的绝缘细线与固定点O连接，AO与电场线垂直处于水平状态，取g="10" m/s2，现让该小球在A处静止释放。
求：（1）小球第一次到达O点正上方时的速度大小和细线的拉力。
（2）若撤去磁场且电场方向转到水平向左，小球仍从A处静止释放，求小球第一次到达O点正下方时增加的机械能△E和速度的大小。（结果可保留根号）
答案
（1）
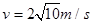T=3.4N（2）△E= 24J；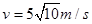
题目分析：（1）在运动过程中小球受到重力，电场力，洛伦兹力，其中洛伦兹力不做功，当小球第一次到达O点正上方时，重力做负功，电场力做正功，根据动能定理可得：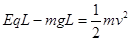
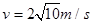，解得解得（3分；
在最高点受到绳子的竖直向下的拉力T，竖直向下的重力mg，竖直向上的洛伦兹力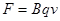
，竖直向上的电场力，四个力的合力充当向心力，
故
,解得T="3.4N" （3分）
（2）过程中电场力做正功，增加的机械能等于减小的电势能，所以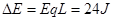
,
△E= 24J（2分）；
小球此时向下开始运动，所以重力正功，故根据动能定理可得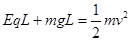
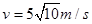解得（2分）
点评：做类型的题目关键是弄清楚粒子的受力情况，结合牛顿第二定律以及动能定理分析
