问题
计算题
(12分)如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一个压敏电阻元件,其阻值与其两端所加电压成正比,即R=kU,式中k为已知的常数.框架上有一质量为m,离地高为h的金属棒,金属棒与框架始终接触良好无摩擦,且保持水平,磁感应强度为B的匀强磁场,方向垂直于框架平面向里.今将金属棒由静止释放,棒沿框架向下运动,不计金属棒电阻,重力加速度为g.试求:

(1)金属棒运动过程中,流过棒的电流大小和方向;
(2)金属棒落到地面时的速度大小;
(3)金属棒从释放到落地过程中通过电子元件的电量.
答案
(1)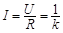 (从a→b)(2)
(从a→b)(2)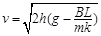 (3)
(3)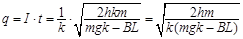
题目分析:(1)流过电阻R的电流大小为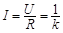 (2分)
(2分)
电流方向水平向右(从a→b) (1分)
(2)在运动过程中金属棒受到的安培力为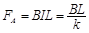 (1分)
(1分)
对金属棒运用牛顿第二定律,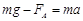 (1分)
(1分)
得: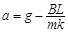 恒定,金属棒作匀加速直线运动 (2分)
恒定,金属棒作匀加速直线运动 (2分)
由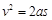 ,得:
,得: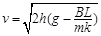 (1分)
(1分)
(3)设金属棒经过时间t落地,由: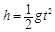 得:
得: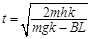 (2分)
(2分)
所求电量: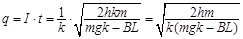 (2分)
(2分)
点评:本题难度中等,特别注意的是压敏电阻的阻值是变化的,由电压与电阻的关系可知流过电阻R的电流恒定不变,因此导体棒的加速度不变,与常规题思路刚好相反

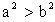 ”的逆命题是( )
”的逆命题是( )