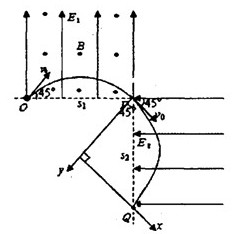
(14分)如图所示,竖直平面内有相互垂直的匀强电场和匀强磁场,电场强度E1=2500 N/C,方向竖直向上;磁感应强度B=103T,方向垂直纸面向外;有一质量m=1×10-2kg、电荷量q=4×10-5C的带正电小球自O点沿与水平线成45°角以v0=4 m/s的速度射入复合场中,之后小球恰好从P点进入电场强度E2=2500 N/C,方向水平向左的第二个匀强电场中.不计空气阻力,g取10 m/s2.求:
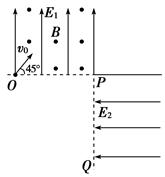
(1)O点到P点的距离s1;
(2)带电小球经过P点的正下方Q点时与P点的距离s2.
(1)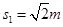 (2)
(2)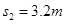
题目分析:分析:(1)粒子在复合场中电场力和重力平衡,则只在洛仑兹力的作用下做匀速圆周运动,由牛顿第二定律可知粒子的半径,由几何关系可得出两点间的距离;
(2)粒子在电场中,由于重力和电场力的作用做类平抛运动,建立合适的坐标系,则可由运动的合成与分解求得两点间的距离.
解:(1)带电小球在正交的匀强电场和匀强磁场中受到重力G=mg=0.1N;
电场力F1=Eq=0.1N
即G=F1,故小球在正交的电场由A到C做匀速圆周运动.
根据牛顿第二定律可知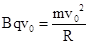
解得: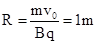
由几何关系得: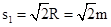 ;
;
(2)带电小球在C点的速度大小仍为v0=4m/s,方向与水平方向成45°.
由于电场力F2=Eq=0.1N
与重力大小相等,方向相互垂直,
则合力的大小为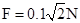 ,方向与初速度垂直,故小球在第二个电场中作平抛运动.
,方向与初速度垂直,故小球在第二个电场中作平抛运动.
建立如图所示的坐标系,沿y方向上,小球的加速度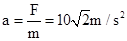 ;
;
位移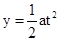
x方向上有小球的位移x=v0t
由几何关系可知:y=x
即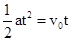 ,
,
解得: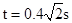
由几何关系可知,Q到P点的距离为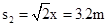 .
.
点评:本题考查带电粒子在复合场中的运动,要注意当粒子在复合场中做匀速圆周运动时,粒子受到的电场力与重力平衡.

 缺失,制作义齿时将模型向后倾斜,可使
缺失,制作义齿时将模型向后倾斜,可使 颊侧形成()。
颊侧形成()。