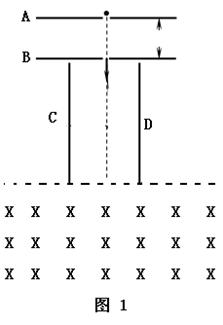
（18分）真空中有如图l装置，水平放置的金属板A、B中间开有小孔，小孔的连线沿竖直放置的金属板C、D的中间线，一质量为m、电荷量为q的带正电粒子（初速不计、重力不计）P进入A、B间被加速后，再进入金属板C、D间的偏转电场偏转，并恰能从D板下边缘射出。已知金属板A、B间电势差为UAB=+U0，C、D板长度均为L，C、D板间距为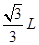
。在金属板C、D下方有如图l所示的、有上边界的、范围足够大的匀强磁场，该磁场上边界与金属板C、D下端重合，其磁感应强度随时间变化的图象如图2，图2中的B0为已知，但其变化周期T未知，忽略偏转电场的边界效应。
（1）求金属板C、D间的电势差UCD；
（2）求粒子刚进入磁场时的速度；
（3）已知垂直纸面向里的磁场方向为正方向，该粒子在图2中t=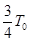
时刻进入磁场，并在t=T0时刻的速度方向恰好水平，求该粒子从射入磁场到离开磁场的总时间t总。
（1）
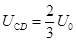（2）
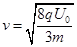，方向与竖直方向夹角为30o
(3) 
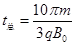
题目分析：（1）设粒子进入偏转电场瞬间的速度为v0，对粒子加速过程由动能定理：
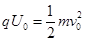得到 
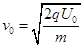（2分）
进入偏转电场中，水平位移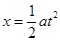
（1分）
其中加速度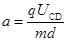
（式中d = 
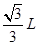） （1分）
竖直位移与时间关系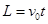
（1分）
又依题意“恰能从D板下边缘射出”：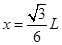 
（1分）
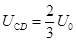解得: （1分）
（2）设粒子进入磁场时的速度为v，对粒子的偏转过程有
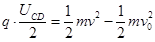（2分）
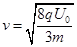解得： （1分）
设粒子由k点离开电场时偏转角为θ，则
解得
（2分）
（3）粒子在磁场中做圆周运动轨迹如图所示，
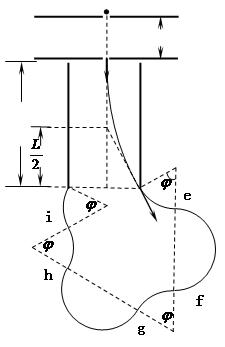
周期为：
（1分）
粒子从k进入磁场沿逆时针方向运动,由“在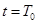
时刻的速度方向恰好水平”知，轨迹对应的圆心角为
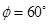，此过程对应的运动时间为
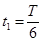，到达了e点；接着磁场反向，在
内粒子沿顺时针方向运动半周到达f点；此时磁场再反向，粒子在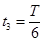
内沿逆时针方向运动到g点；接着在
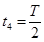内运动到h点；再接着在
内运动到i点；最后经
离开磁场。
则该粒子从射入磁场到离开磁场的总时间为
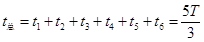（4分）
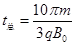即 （1分）