解：（1）由题意知：f'（x）=3mx²+4nx-12＜0的解集为（-2，2），

所以，-2和2为方程3mx²+4nx-12=0的根，

由韦达定理知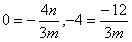，即m=1，n=0。

（2）∵f（x）=x³-12x，

∴f'（x）=3x²-12，

∵f（1）=1³-12·1=-11，

当A为切点时，切线的斜率k=f'（1）=3-12=-9，

∴切线方程为y+11=-9（x-1），即9x+y+2=0；

当A不为切点时，设切点为P（x₀，f（x₀）），这时切线的斜率是k=f'（x₀）=

切线方程为y-f（x₀）=f'（x₀）（x-x₀），

即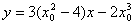

因为过点A（1，-11），

∴

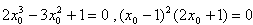
∴x₀=1或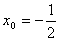，而x₀=1为A点，

即另一个切点为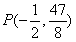

∴

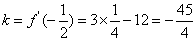
切线方程为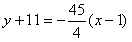，即45x+4y-1=0，

所以，过点A（1，-11）的切线方程为9x+y+2=0或45x+4y-1=0。

（3）存在满足条件的三条切线

设点P（x₀，f（x₀））是曲线f（x）=x³-12x的切点，

则在P点处的切线的方程为y-f（x₀）=f'（x₀）（x-x₀）

即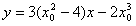

因为其过点A（1，t），

所以，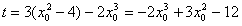

由于有三条切线，所以方程应有3个实根，

设g（x）=2x³-3x²+t+12，只要使曲线有3个零点即可

设g'（x）=6x²-6x=0，

∴x=0或x=1分别为g（x）的极值点，

当x∈（-∞，0）和（1，+∞）时，g'（x）>0，

g（x）在（-∞，0）和（1，+∞）上分别单增，

当x∈（0，1）时，g'（x）＜0，g（x）在（0，1）上单减，

所以，x=0为极大值点，x=1为极小值点，

所以要使曲线与x轴有3个交点，

当且仅当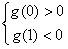即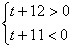

解得-12＜t＜-11。