问题
计算题
在某回旋加速器中，磁场的磁感应强度为B，粒子源射出的粒子质量为m，电荷量为q，粒子的最大回旋半径为Rm，问：
(1)D形盒内有无电场？
(2)粒子在盒内做何种运动？
(3)所加交变电场的周期是多大？
(4)粒子离开加速器时能量是多大？
(5)设两D形盒间电场的电势差为U，盒间距离为d，其间电场均匀，求把静止粒子加速到上述能量所需的时间。
答案
解：(1)D形盒由金属导体制成，具有屏蔽外电场的作用，盒内无电场
(2)带电粒子在盒内做匀速圆周运动，每次加速后轨道半径增大
(3)交变电场的周期应与粒子旋转的周期相同，即
(4)粒子离开加速器时达到最大速度vm，由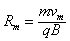
，可得vm=
则其动能为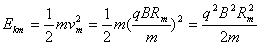
(5)设粒子达到最大动能须经n次加速，则粒子在回旋加速器中运动的时间t应为在D形盒内的回旋时间t1与通过D形盒间的缝隙的加速时间t2之和，即t=t1+t2
由nqU=Ekm，得n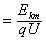
则粒子旋转的周期数为粒子在两D形盒缝隙中加速时，受到的电场力为
，运动的加速度
，质子n次通过缝隙的总位移为s=nd，由于质子n次加速的过程可视为初速度为零的匀加速直线运动，故有（注意等效的思想方法）
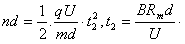
所以