问题
计算题
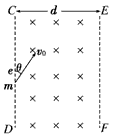
匀强磁场的磁感应强度为B，宽度为d，边界为CD和EF。一电子从CD边界外侧以速率v0垂直射入匀强磁场，入射方向与CD边界间夹角为θ。已知电子的质量为m，电荷量为e，为使电子能从磁场的另一侧EF射出，求电子的速率v0至少多大？若θ角可取任意值，v0的最小值是多少？
答案
解：本题考查圆周运动的边界问题的求解方法。当入射速率v0很小时，电子会在磁场中转动一段圆弧后又从CD一侧射出，速率越大，轨道半径越大，当轨道与边界EF相切时，电子恰好不能从EF射出，如图所示。电子恰好射出时，由几何知识可得：
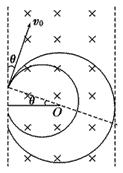
r＋rcosθ＝d ①
又r＝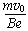
②
由①②得v0＝
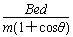③
故电子要射出磁场，速率至少应为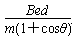
由③式可知，θ＝0°时，v0＝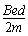
最小
由②式知此时半径最小，rmin＝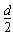
，也可由轨迹分析得出上述结论