问题
单项选择题
设
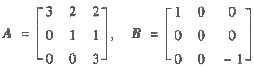，若矩阵x满足：AX+2B=BA+2X，则X4=
答案
参考答案：B
解析：
[分析]： 由题设矩阵方程，得 (A-2E)X=B(A-2E)．
因为[*]可逆，故X=(A-2E)-1B(A-2E)．
从而X4=(A-2E)-1B4(A-2E)
=[*]
所以应选(B)．
[*]
搜题请搜索小程序“爱下问搜题”
设
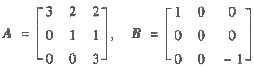，若矩阵x满足：AX+2B=BA+2X，则X4=
参考答案：B
解析：
[分析]： 由题设矩阵方程，得 (A-2E)X=B(A-2E)．
因为[*]可逆，故X=(A-2E)-1B(A-2E)．
从而X4=(A-2E)-1B4(A-2E)
=[*]
所以应选(B)．
[*]