问题
计算题
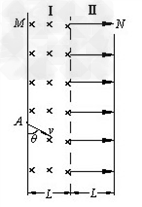
在真空室内，竖直放置的M、N板涂有荧光物质，如图所示．两板间竖直条形区域Ⅰ存在垂直纸面向里的匀强磁场，区域Ⅱ存在水平向右的匀强电场，磁场和电场均有界，宽度均为L，且足够长，磁场的强弱可以调节，电场强度恒为E．现有一束质子从A处连续不断地射入磁场，入射方向与M板成θ= 60°夹角且与纸面平行，已知该质子束由两种速度的质子组成，一种速度大小为v的低速质子，另一种速度大小为3v的高速质子．当Ⅰ区域的磁场较强时，M板出现两个亮斑，缓慢改变磁场强弱，直到两个亮斑相继消失，此时观察到N板有两个亮斑．已知质子质量为m，电量为e，不计质子重力和相互间作用力，求：
（1）若保持M、N板各有一个亮斑，磁场的磁感应强度应控制在什么范围内；
（2）当M板亮斑刚好消失，N板出现两个亮斑时，两个亮斑之间的距离．
答案
解：（1）M、N板各有一个亮斑，高速质子打在N板上，低速质子打在M板上．B最大时，高速质子速度恰好与两场交界相切且与电场方向垂直，在磁场中运动半径为R1，则有
解得
B最小时，低速质子速度恰好与两场交界相切且与电场方向垂直，在磁场中运动半径为R2，则有
解得
磁感应强度的取值范围为：
（2）恰好出现两个亮斑时，低速质子速度恰好与两场交界相切且与电场方向垂直，在磁场中运动半径为R2，高速质子半径
，轨迹如图所示．由几何关系知此时高速质子沿电场线方向进入电场，到达N板时与A点得竖直高度差为
低速质子在磁场中偏转距离为
设在电场中运动时间为
，则有
，
在电场中偏转的距离为
解以上各式得
加富含蛋白质的食物是 （只填一种）；