问题
问答题
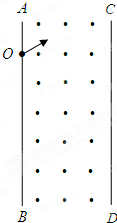
如图所示,在两平行边AB CD的狭长区域内,分布有磁感应强度B=1T而方向垂直纸面向外的匀强磁场,磁场区域宽度d=2cm.一带正电的粒子,质量m=3.2×10-27kg,带电量q=1.6×10-19Cv,以速v=2×106m/s从左边界的O处斜向上射入磁场,粒子刚好从另一边界垂直射出,求:
(1)请画出带电粒子在磁场中运动的运动轨迹
(2)带电粒子在磁场中的轨道半径r为多大?
(3)带电粒子在磁场中的运动时间t是多少?
(此小题结果保留三位有效数字)
答案
(1)粒子在磁场中的运动轨迹如图所示
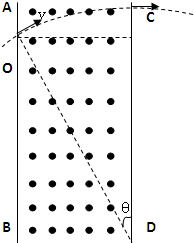
(2)带电粒子在磁场中做匀速圆周运动,
根据牛顿第二定律,有:qvB=mv2 r
解得:r=
=mv qB
m=4×10-2m3.2×10-27×2×106 1.6×10-19×1
(3)由几何关系得:
sinθ=
=d r
=0.5 2×10-2 4×10-2
即θ=30°
故带电粒子在磁场中运动的时间为:t=
T=30° 360° 2πm 12qB
=
s=1.05×10-8s2×3.14×3.2×10-27 12×1.6×10-19×1
答:(1)带电粒子在磁场中运动的运动轨迹如上图;
(2)带电粒子在磁场中的轨道半径r为4×10-2m;
(3)带电粒子在磁场中的运动时间t是1.05×10-8s.
