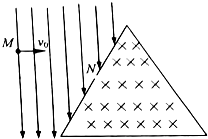
如图所示,横截面是边长为a的等边三角形的管道内有垂直于纸面向里的匀强磁场,N为处于三角形一边中点的小孔.管道外有方向竖直向下,电场强度为E的匀强电场.质量为m、电荷世为q的带止电粒子自M点以水平初速度v0进入电场区域,已知粒子恰好从N孔垂直该边进入磁场区域,粒子与管道发生两次碰撞后仍从N孔射出,设粒子与管道碰撞过程中没有能量损失,且电荷量保持不变,不计粒子重力,求:
(1)粒子由M到N的水平距离;
(2)磁场的磁感应强度B;
(3)粒子由M点出发到第二次到达N孔所用的时间.
(1)粒子由M到N做类平抛运动,
加速度:a=,
竖直分速度vy=at1=,
在N点,tan30°===,
解得:t1=,
粒子的水平位移:x=v0t1=;
(2)粒子在磁场中做匀速圆周运动,
由几何知识可知,其轨道半径:R=,
由牛顿第二定律得:qvB=m,
速度:v==,
解得:B=;
(3)在匀强磁场中,粒子做匀速圆周运动,
由牛顿第二定律得:qvB=m()2R,
粒子做圆周运动的周期:T=,
在磁场中运动的时间为半周期,
粒子运动时间:t2===,
粒子总的运动时间:t=t1+t2,
t=+;
答:(1)粒子由M到N的水平距离为;
(2)磁场的磁感应强度B=;
(3)粒子由M点出发到第二次到达N孔所用的时间t=+.

