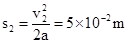问题
计算题
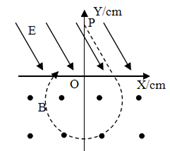
如图所示，在直角坐标系XOY平面内,在Y＞0处有与X轴成60°角的匀强电场，场强大小E=103v/m，在Y＜0处有垂直于纸面向外的匀强磁场，磁感应强度B=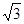
T。现从t=0时刻在坐标为(0,10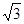cm)的P点由静止释放一比荷为104C/kg的带正电的微粒A，不计微粒的重力。求：
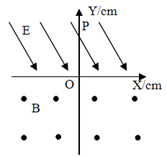
（1）微粒进入磁场后在磁场中运动的半径；
（2）第二次穿过X轴的时刻；
（3）在释放微粒A后又在电场中由静止释放另一个与A完全相同的微粒B，若要使微粒A在第二次穿过X轴到第三次穿过X轴的时间内与微粒B相遇，求微粒B释放的时刻和释放的位置。
答案
（1）
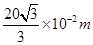（2）
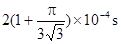
（3）在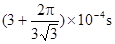
时刻由静止释放B
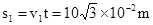
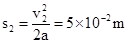
（1）释放A微粒后在电场中沿电场方向做匀加速直线运动
由：EqL=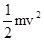
得：v=2×103m/s
由：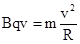
得：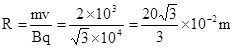
(2)由几何关系可知：A在磁场中运动的圆心坐标为（0，－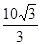
cm）
A进入磁场前运动的时间t1：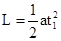
得：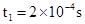
A进入磁场中运动的时间t2：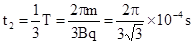
故在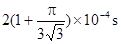时刻A第二次穿过X轴
（3）设A第二次从Q穿过X轴，此时速度方向与X轴正方向成60°角，将此速度分解为垂直电场方向的速度V1和平行于电场方向V2。
在沿电场方向由：V2=at3
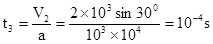
故在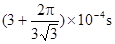时刻由静止释放B
垂直电场方向的位移：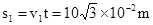
沿电场方向的位移：
