问题
解答题
已知一个等腰三角形的周长为18cm．
（1）如果腰长是底边的2倍，那么各边的长是多少？
（2）如果一腰上的中线将该等腰三角形的周长分为1：2两部分，那么各边的长为多少？
答案
（1）
设底边BC=acm，则AC=AB=2acm，
∵三角形的周长是18cm，
∴2a+2a+a=18，
∴a=
，2a=18 5
，36 5
答：等腰三角形的三边长是
cm，18 5
cm，36 5
cm．36 5
（2）
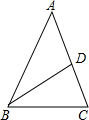
设BC=acm，AB=AC=2bcm，
∵中线BD将△ABC的周长分为1：2两部分，18×
=12，18×2 3
=6，1 3
∴2b+b=6，b+a=12或2b+b=12，b+a=6，
解得：a=10，b=2或b=4，a=2，
∴①三角形三边长是10cm，4cm，4cm，
因为4+4＜10，不符合三角形三边关系定理，
∴此种情况舍去，
②三角形的三边长是2cm，8cm，8cm，
符合三角形的三边关系定理，
综合上述：符合条件的三角形三边长是8cm，8cm，2cm，
答：等腰三角形的边长是8cm，8cm，2cm．