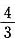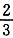因为ω=cos

π

5

+isin

π

5

，所以ω⁵+1=(cos

π

5

+isin

π

5

)5+1=cosπ+isinπ+1=0，

所以ω=cos

π

5

+isin

π

5

是方程x⁵+1=0的一个根，

因为-1=cosπ+isinπ，

则-1的5次方根为coc

π+2kπ

5

+isin

π+2kπ

5

（k=0，1，2，3，4），

当k=0时为ω，当k=1时为ω³，当k=3时为ω⁷，当k=4时为ω⁹，

而x⁵+1=（x+1）（x⁴-x³+x²-x+1）=0，

故ω，ω³，ω⁷，ω⁹ 都是方程x⁴-x³+x²-x+1=0．

故选B．