(15分)真空中有一半径为r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里,Ox为过边界上O点的切线,如图所示,从O点在纸面内向各个方向发射速率均为v0的电子,设电子间相互作用忽略,且电子在磁场中偏转半径也为r.已知电子的电量为e,质量为m.
(1)圆柱形区域匀强磁场的磁感应强度大小为多少?
(2)速度方向与Ox方向夹角成90°的电子,在磁场中的运动时间为多少?
(3)在x轴上有一点p,距O点的距离为3r,要使从O点发射的速率均为v0的电子,从磁场边界出来后都能够汇聚到p点,请在图中虚线MN右侧添加一个匀强磁场,并说明磁感应强度大小和方向及分布情况。
(1)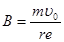 (2)
(2) (3)
(3)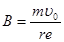 方向垂直于纸面向里
方向垂直于纸面向里
区域:与X轴相切于P点,在X轴上方,半径为r的圆
题目分析:(1)粒子进入磁场后,根据洛伦兹力提供向心力 可得
可得 ,所以
,所以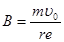 。
。
(2)速度方向与Ox方向夹角成90°的电子,进入垂直于纸面向里的磁场,根据左手定则判断电子在磁场中运动圆心角为90°相当于0.25个周期。
根据洛伦兹力提供向心力, ,且
,且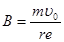 ,所以
,所以
(3)为了使从O点发射的速率均为v0的电子,从磁场边界出来后都能够汇聚到p点,需要施加如答案的圆形区域磁场。
点评:此类题型考察了洛伦兹力提供向心力,并考察了粒子在磁场中的运动轨迹的圆心角,此类题型的常见做法是定圆心,找半径、画轨迹,本题属于比较经典的题型。
