问题
计算题
（18分）如图，在0≤x≤d的空间，存在垂直xOy平面的匀强磁场，方向垂直xOy平面向里。y轴上P点有一小孔，可以向y轴右侧垂直于磁场方向不断发射速率均为v、与y轴所成夹角θ可在0~1800范围内变化的带负电的粒子。已知θ =450时，粒子恰好从磁场右边界与P点等高的Q点射出磁场，不计重力及粒子间的相互作用。求
（1）磁场的磁感应强度；
（2）若θ=300，粒子射出磁场时与磁场边界的夹角（可用三角函数、根式表示）；
（3）能够从磁场右边界射出的粒子在磁场中经过的区域的面积（可用根式表示）。
答案
（1）B=
（2）cosα=
，（3）
题目分析：1）粒子在磁场中做匀速圆周运动，设粒子的轨道半径为R，磁场的磁感应
强度为B,则
qvB=m
（3分）
如下图实线所示，由几何关系
d=2Rcos450 （3分）
解得 B= （2分）
（2）如上图虚线所示，由几何关系
d=Rcos300+Rcosα （2分）
解得 cosα= （2分）
(3) 能够从磁场右边界射出的粒子在磁场中经过的区域,如图中两圆弧间斜线部分所示，由几何关系
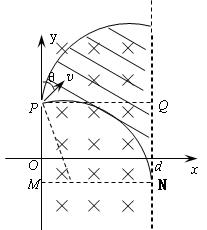
R2- (d-R)2 =(PM)2 （2分）
两个圆弧与水平线之间围成的面积是相等的，所以所求区域面积与矩形PQMN的面积
（2分）
解得 （2分）
