已知数列{an}中，a1=1，an+1-an=
|
因为an=(an-an-1)+(an-1+an-2)++(a2-a1)+a1=
+1 3n
++1 3n-1
+11 32
所以an是一个等比数列的前n项和，所以an=
，且q=2．代入，1-qn 1-q
所以
an=1+lim n→∞
=1 32 1- 1 3
．7 6
所以答案为7 6
某同学在学习“硫酸及其盐的某些性质与用途“中，进行如下实验探究．
【实验一】探究浓硫酸的氧化性
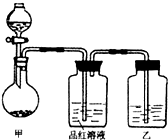
将实验室常用的药品放入如右图所示的实验装置后，加热装置甲．（夹持和加热装置省略）
（1）该装置设计上存在明显缺陷，请指出：______．
（2）写出装置甲中反应的化学方程式______．
（3）装置乙中的试剂是______．
【实验二】探究某硫酸亚铁盐固体是否变质
（4）请你帮助该同学完成如下实验方案：
| 实验操作 | 预期现象和结论 |
查阅资料得知：工业上用电解KHSO4饱和溶液制取H2O2，示意图如图：
该同学用此法制取一定浓度的H2O2，并进行下列实验测定H2O2的质量分数．
①取5.00mL H2O2溶液（密度为1.00g/mL）置于锥形瓶中加水稀释，再加稀硫酸酸化；
②用0.1000mol/L KMnO4溶液滴定；
③用同样方法滴定，三次消耗KMnO4溶液的体积分别为20.00mL、19.98mL、20.02mL．
回答下列问题：
（5）电解饱和KHSO4溶液时，阳极的电极反应式为______．
（6）操作②中，滴入第一滴KMnO4溶液，溶液紫红色消失很慢，随着滴定过程中Mn2+的增多，溶液紫红色消失速率加快．Mn2+的作用是______．
（7）写出该滴定反应的离子方程式：______．
（8）原H2O2溶液中溶质的质量分数为______．
