搜题请搜索小程序“爱下问搜题”
问题 填空题
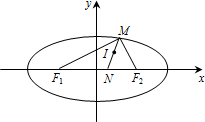
已知M是椭圆
x2
9
+
y2
5
=1上一点，F1，F2是椭圆的两个焦点，I是△MF1F2的内心，延长MI交F1F2于N，则
|MI|
|NI|
等于______．
答案

如图，连接IF1，IF2．在△MF1I中，F1I是∠MF1N的角平分线，

根据三角形内角平分线性质定理，

|MI|
|NI|
=
|MF1|
|F1N|
，同理可得
|MI|
|NI|
=
|MF2|
|F2N|
，

∴

|MI|
|NI|
=
|MF1|
|F1N|
=
|MF2|
|F2N|
；

根据等比定理

|MI|
|NI|
=
|MF1|+|MF2|
|F1N|+|F2N|
=
2a
2c
=
2×3
2×
9-5
=
3
2
．

故答案为：

3
2
．

单项选择题

男性，55岁。被汽车撞倒半小时，昏迷状态。急诊平扫CT。检查图像如图所示，诊断最可能是（）

A.脑实质出血

B.正常脑CT表现

C.硬膜下血肿

D.硬膜外血肿

E.蛛网膜下隙出血
查看答案
单项选择题

为了验证财务报表上存货项目余额的存在，注册会计师A除了对企业存货的结存数量子以确认外，还应当进行( )。

A．审查存货盘亏或损失处理

B．进行采购业务的年底测试

C．进行存货计价测试

D．实地观察存货盘点
查看答案