问题
选择题
按照我国月球探测活动计划，在第一步“绕月”工程圆满完成任务后，将开展第二步“落月”工程，预计在2013年前完成．假设月球半径为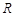
，月球表面的重力加速度为
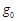.飞船沿距月球表面高度为3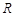的圆形轨道Ⅰ运动，到达轨道的
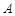点，点火变轨进入椭圆轨道Ⅱ，到达轨道Ⅱ的近月点
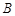再次点火进入近月轨道Ⅲ绕月球做圆周运动．下列判断正确的是
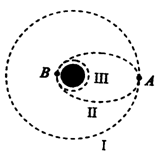
A．飞船在轨道Ⅰ上的运行速率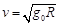
B．飞船在轨道Ⅲ绕月球运动一周所需的时间为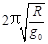
C．飞船在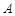点点火变轨的瞬间，动能减小
D．飞船在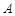点的线速度大于在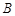点的线速度
答案
BC
考点：
分析：在月球表面，万有引力等于重力，在任意轨道，万有引力提供向心力，联立方程即可求解，
卫星变轨也就是近心运动或离心运动，根据提供的万有引力和所需的向心力关系确定．
飞船在近月轨道Ⅲ绕月球运行，重力提供向心力，根据向心力周期公式即可求解
解答：解：A、飞船在轨道Ⅰ上，万有引力提供向心力：
GMm/(4R) 2=m v2/4R
在月球表面，万有引力等于重力得：
GMm/ R2=mg0，解得：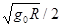
，故A错误．
B、设飞船在近月轨道Ⅲ绕月球运行一周所需的时间为T，则：
m4π2/T2R=mg0，
T=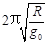
，故B正确．
C、在圆轨道实施变轨成椭圆轨道远地点是做逐渐靠近圆心的运动，要实现这个运动必须万有引力大于飞船所需向心力，所以应给飞船点火减速，减小所需的向心力．故C正确．
D、飞船在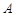
点的线速度小于在
点的线速度，故D错误
故选BC．
点评：该题考查了万有引力公式及向心力基本公式的应用，难度不大，属于中档题．