问题
解答题
设函数f(x)=x(x-1)(x-a),(a>1)求导数f′(x); 并证明f(x)有两个不同的极值点x1,x2.
答案
f′(x)=(x-1)(x-a)+x(x-a)+x(x-1)=3x2-2(a+1)x+a,
∵△=4(a+1)2-12a=4a2-4a+4=4(a-
)2+3>0,1 2
∴f′(x)=0必有两个不同实根x1,x2,(不妨设x1<x2)
又∵f′(x)=的图象开口向上,
∴-∞<x<x1,或x2<x<+∞时,f′(x)>0,
x1<x<x2时,f′(x)<0,
∴f(x)有两个不同的极值点x1,x2


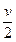 的速度向右运动
的速度向右运动