问题
计算题
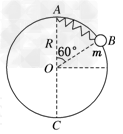
一个质量m=0.2 kg的小球系于轻质弹簧的一端,且套在光滑竖立的圆环上,弹簧的上端固定于环的最高点A,环的半径R=0.5 m,弹簧的原长l0=0.5 m,劲度系数为4.8 N/m,如图所示.若小球从图中所示位置B点由静止开始滑动到最低点C时,弹簧的弹性势能E弹=0.60 J.求:(g取10 m/s2)
(1)小球到达C点时的速度vC的大小;
(2)小球在C点对环的作用力.
答案
解:(1)小球在B点时弹簧的长度为l1=R=l0
所以在此位置时弹簧处于自然状态,弹簧的弹性势能等于零
小球由B点滑到C点的过程中,由能量守恒定律得:mgR(1+cos60°)= mvC2+E弹
mvC2+E弹
可解得vC=3.0 m/s
(2)设环对球在C点的作用力为F,方向竖直向上

如图所示,由牛顿第二定律有F弹+F-mg=m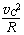
由胡克定律有:F弹=k(2R-l0)
由以上两式可解得:F=3.2 N
由牛顿第三定律可知,球对环的作用力与F等值反向
