问题
填空题
已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a、b、c三个向量共面,则实数λ等于________.
答案
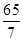
由于a、b、c三个向量共面,所以存在实数m、n使得c=ma+nb,即有(7,5,λ)=m(2,-1,3)+n(-1,4,-2),即(7,5,λ)=(2m-n,-m+4n,3m-2n),∴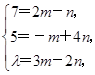 解得m=
解得m=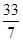 ,n=
,n=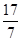 ,λ=
,λ=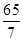 .
.
已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a、b、c三个向量共面,则实数λ等于________.
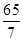
由于a、b、c三个向量共面,所以存在实数m、n使得c=ma+nb,即有(7,5,λ)=m(2,-1,3)+n(-1,4,-2),即(7,5,λ)=(2m-n,-m+4n,3m-2n),∴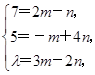 解得m=
解得m=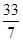 ,n=
,n=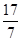 ,λ=
,λ=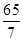 .
.