问题
问答题
如图所示,AB为水平轨道,A、B间距离x="2.25" m ,BCD是半径为R=0.40 m的竖直半圆形轨道,B为两轨道的连接点,D为轨道的最高点。一小物块质量为m="1." 2 kg,它与水平轨道和半圆形轨道间的动摩擦因数均为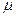 =" 0." 20。小物块在F="12" N的水平力作用下从A点由静止开始运动,到达B点时撤去力F,小物块刚好能到达D点,g取10
=" 0." 20。小物块在F="12" N的水平力作用下从A点由静止开始运动,到达B点时撤去力F,小物块刚好能到达D点,g取10 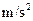 ,试求:
,试求:
(1)撤去F时小物块的速度大小;
(2)在半圆形轨道上小物块克服摩擦力做的功。
答案
v="6" m/s,在圆形轨道上小物块克服摩擦力做的功为9. 6 J。
(1)用动能定理求解
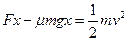 ①
①
v="6" m/s ②
(2)设小物块到达D点时的速度为 ,又因为小物块恰能到达D点
,又因为小物块恰能到达D点
所以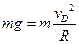
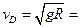 2 m/s
2 m/s
设重力和摩擦力所做的功分别为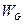 和
和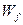 ,由动能定理
,由动能定理
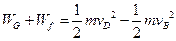
 9.6J
9.6J
所以在圆形轨道上小物块克服摩擦力做的功为9. 6 J。
