问题
问答题
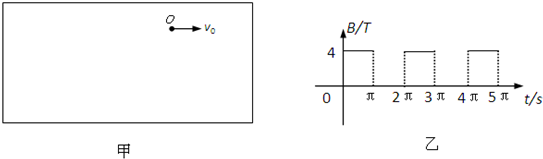
图甲是一足够大的光滑绝缘水平面,在t=0时刻,质量m=0.04kg、电荷量q=0.01C的带负电小球以初速度v0=1m/s从Ο点开始水平向右运动.整个平面处于方向竖直向下的匀强磁场中.
(1)若磁感应强度B=4T并保持不变,求小球在匀强磁场中运动的半径和周期.
(2)若从t=0时刻开始,磁感应强度B随时间的变化规律如图乙所示,求小球至少经过多长时间才能再次经过Ο点,画出小球在这段时间内的运动轨迹并求小球通过的路程.
答案
(1)小球所受洛伦兹力提供做匀速圆周运动的向心力qv0B=mv02 R
则小球在磁场中的运动半径R=
=1mmv0 qB
小球在磁场中的运动周期T=
=2πs2πR v0
(2)在有磁场存在的半个周期内,磁感应强度B=4T,
因此小球做匀速圆周运动的半径和周期与前面相同,t=π s=
,因此小球运动了半周;T 2
在没有磁场存在的半个周期内,小球做匀速直线运动.
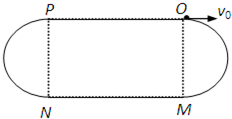
小球在0~4πs的时间内的运动轨迹如图
因此小球再次经过O点,经过的时间至少为
t=tOM+tMN+tNP+tPO=4π s
因此小球再次经过O点,通过的路程
s=sOM+sMN+sNP+sPO=4π m
或因为小球的速率保持不变,因此通过的路程为s=v0t=4π m
答:小球在匀强磁场中运动的半径为1m,周期为2πs;(2)小球至少经过4πs才能再次经过Ο点,小球通过的路程为4π m.
