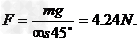问题
计算题
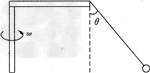
如图所示,已知绳长L=20cm,水平杆长L'=0.1m,小球质量m=0.3kg,整个装置可以绕竖直转轴转动,问:
(1)要使绳子与竖直方向成45°角,该装置必须以多大的角速度转动才行?
(2)此时绳子的拉力为多大?
答案
解:小球绕杆做圆周运动,其轨道平面在水平面内,
轨道半径r=L'+Lsin 45°,
绳的拉力与小球重力的合力提供小球做圆周运动的向心力,
对小球的受力分析如图所示.
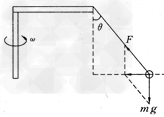
设绳对小球拉力为F,重力为mg,
则绳的拉力与重力的合力提供小球做圆周运动的向心力,
利用牛顿第二定律可得:mgtan45°=mω2r,r=L'+Lsin 45°
联立以上两式,代入数据可得:ω= 6. 4 rad/s,