(The Guardian): More UK universities should be profiting from ideas
A repeated criticism of the UK's university sector is its noticeable weakness in translating new knowledge into new products and services.
Recently, the UK National Stem Cell Network warned the UK could lose its place among the world leaders in stem cell research unless adequate funding and legislation could be assured, despite an annual £40m spent by the Department of Health on all kinds of research.
However, we do have to challenge the unthinking complaint that the sector does not do enough in taking ideas to market. The most recent comparative data on the performance of universities and research institutions in Australia, Canada, USA and UK shows that, from a relatively weak starting position, the UK now leads on many indicators of commercialization activity.
When viewed at the national level, the policy interventions (interference) of the past decade have helped transformed the performances of UK universities. Evidence suggests the UK's position is much stronger than in the recent past and is still showing improvement. But national data masks the very large variation in the performance of individual universities. The evidence shows that a large number of universities have fallen off the back of the pack, a few perform strongly and the rest chase the leaders.
This type of uneven distribution is not strange to the UK and is mirrored across other economies. In the UK, research is concentrated: less than 25% of universities are receiving 75% of the research funding. These same universities are also the institutions producing the greatest share of PhD graduates, science citations, patents and license income. The effect of policies generating long-term resource concentration has also created a distinctive set of universities which are research-led and commercially active. It seems clear that the concentration of research and commercialization work creates differences between universities.
The core objective for universities which are research-led must be to maximize the impact of their research efforts. Their purpose is not to generate funds to add to the bottom line of the university or to substitute other income streams. Rather, these universities should be generating the widest range of social, economic and environmental benefits. In return for the scale of investment, they should share their expertise (expert knowledge or skill) in order to build greater confidence in the sector.
Part of the economic recovery of the UK will be driven by the next generation of research commercialization spilling out of our universities. On the evidence presented in my report, there are three dozen universities in the UK which are actively engaged in advanced research training and commercialization work.
If there was a greater coordination(协调)of technology transfer offices within regions and a simultaneous (happening at the same time) investment in the scale and functions of our graduate schools, universities could, and should, play a key role in positioning the UK for the next growth cycle.
小题1:What does the author think of UK universities in terms of commercialization?
A.They have lost their leading position in many ways.
B.They still have a place among the world leaders.
C.They do not regard it as their responsibility.
D.They fail to change knowledge into money.小题2:What does the author say about the national data on UK universities’ performance in commercialization?
A.It masks the fatal weaknesses of government policy.
B.It indicates their ineffective use of government resources.
C.It does not rank UK universities in a scientific way.
D.It does not reflect the differences among universities.小题3:We can infer from Paragraph 5 that “policy interventions (in Paragraph 4)” refers to _____.
A.concentration of resources in a limited number of universities
B.compulsory cooperation between universities and industries
C.government aid to non-research-oriented universities
D.fair distribution of funding for universities and research institutions小题4:What dose the author suggest research-led universities do?
A.Fully use their research to benefit all sectors of society.
B.Generously share their facilities with those short of funds.
C.Advertise their research to win international recognition.
D.Spread their influence among top research institutions.
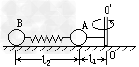
 劲度系数为K的弹簧相连,一长为l1的细线与m1相连,置于水平光滑桌面上,细线的另一端拴在竖直轴OO′上,如图所示,当m1与m2均以角速度ω绕OO′做匀速圆周运动时,弹簧长度为l2。求:
劲度系数为K的弹簧相连,一长为l1的细线与m1相连,置于水平光滑桌面上,细线的另一端拴在竖直轴OO′上,如图所示,当m1与m2均以角速度ω绕OO′做匀速圆周运动时,弹簧长度为l2。求: