如图,xOy平面内存在着沿y轴正方向的匀强电场.一个质量为m,带电荷量为+q的粒子从坐标原点O以速度v0沿x轴正方向开始运动.当它经过图中虚线上的M(2
a,a)点时,撤去电场,粒子继续运动一段时间后进入一个矩形匀强磁场区域(图中未画出),又从虚线上的某一位置N处y轴负方向运动并再次经过M点.已知磁场方向垂直xOy平面(纸面)向里,磁感应强度大小为B,不计粒子的重力.试求:3
(1)电场强度的大小;
(2)N点的坐标;
(3)矩形磁场的最小面积.
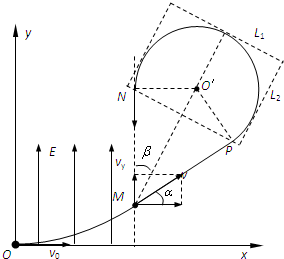
如图是粒子的运动过程示意图.
(1)粒子从O到M做类平抛运动,设时间为t,则有
2
a=v0t 3
a=
×1 2
t2 qE m
得E=mv02 6qa
电场强度大小为:E=mv2 6qa
(2)设粒子运动到M点时速度为v,与x方向的夹角为α,则:vy=
t=qE m
v0 3 3
v=
=
+v 20 v 2y
v0 2 3 3
tanα=
=vy v0
,即α=300,3 3
由题意知,粒子从P点进入磁场,从N点离开磁场,粒子在
磁场中以O′点为圆心做匀速圆周运动,设半径为R,
则:qBv=m
,v2 R
代入数据得粒子做圆周运动的半径为:
R=
=mv qB 2
mv03 3qB
由几何关系知:β=
∠PMN=300 1 2
所以N点的纵坐标为yN=
+a=R tanβ
+a 2mv0 qB
横坐标为xN=2
a 3
故N点的坐标为(2
a,3
+a)2πv0 qB
(3)当矩形磁场为图示虚线矩形时的面积最小.则矩形的两个边长分别为
L1=2R=4
mv03 3qB
L2=R+Rsinβ=
mv03 qB
所以矩形磁场的最小面积为:Smin=L1×L2=4m2 v 20 q2B2
矩形磁场最小面积为Smin=4m2 v 20 q2B2
