问题
选择题
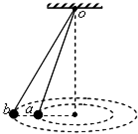
如图所示,两个质量相同的小球a、b用长度不同的细绳悬挂在天花板的O点,分别给每个小球一个合适的初速度,使两小球在同一水平面内做匀速圆周运动,下列关于两球的说法中正确的是( )
A.两球的线速度相等
B.两球的周期相等
C.两球的加速度相等
D.两条细线的拉力相等
答案
对其中一个小球受力分析,如图,受重力,绳子的拉力,由于小球做匀速圆周运动,故合力提供向心力;
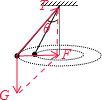
将重力与拉力合成,合力指向圆心,由几何关系得,
细线的拉力T=
,因为b球与竖直方向的夹角大于a求与竖直方向的夹角,所以b绳的拉力大,故D错误;mg cosθ
合力:F=mgtanθ ①;
由向心力公式得到,F=mω2r ②;
设绳子与悬挂点间的高度差为h,由几何关系,得:r=htanθ ③;
由①②③三式得,ω=
.知角速度相等.g h
由T=
知,角速度相同,则周期相同.故B正确.2π ω
由v=wr,a球的半径小于b球的半径,则a球的线速度小于b球的线速度.故A错误.
由a=ω2r,a球的半径小于b球的半径,则a球的加速度小于b球的加速度.故C错误.
故选B.
