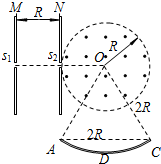
如图所示，相距为R的两块平行金属板M、N正对着放置，s1、s2分别为M、N板上的小孔，s1、s2、O三点共线，它们的连线垂直M、N，且s2O=R．以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向外的匀强磁场．D为收集板，收集板上各点到O点的距离以及两端点A和C的距离都为2R，板两端点的连线AC垂直M、N板．质量为m、带电量为+q的粒子，经s1进入M、N间的电场后，通过s2进入磁场．粒子在s1处的速度和粒子所受的重力均不计．
（1）当M、N间的电压为Ux时，求粒子进入磁场时速度的大小vx；
（2）要使粒子能够打在收集板D上，求在M、N间所加电压的范围；
（3）若粒子恰好打在收集板D的中点上，求粒子从s1开始运动到打在D的中点上经历的时间．
（1）粒子从s1到达s2的过程中，根据动能定理得：qUx=
mvx21 2
解得：vx=2qUx m
（2）粒子进入磁场后在洛伦兹力作用下做匀速圆周运动，设此时其速度大小为v，轨道半径为r，根据牛顿第二定律得：qvB=mv2 r
粒子在M、N之间运动，根据动能定理得：qU=
mv2，1 2
联立解得：U=qB2r2 2m
当粒子打在收集板D的A点时，经历的时间最长，由几何关系可知粒子在磁场中运动的半径r1=
R，此时M、N间的电压最小，为U1=3 3 qB2R2 6m
当粒子打在收集板D的C点时，经历的时间最短，由几何关系可知粒子在磁场中运动的半径r2=
R，此时M、N间的电压最大，为U2=3 3qB2R2 2m
要使粒子能够打在收集板D上，在M、N间所加电压的范围为
≤U≤qB2R2 6m
．3qB2R2 2m
（3）根据题意分析可知，当粒子打在收集板D的中点上时，根据几何关系可以求得粒子在磁场中运动的半径r0=R，粒子进入磁场时的速度v0=qBr0 m
粒子在电场中运动的时间：t1=R v0 2
粒子在磁场中做匀速圆周运动的周期T=
=2πr0 v0 2πm qB
粒子在磁场中经历的时间t2=
T1 4
粒子出磁场后做匀速直线运动经历的时间t3=R v0
所以粒子从s1运动到A点经历的时间为t=t1+t2+t3=(6+π)m 2qB
答：（1）当M、N间的电压为Ux时，求粒子进入磁场时速度的大小vx=
；2qUx m
（2）要使粒子能够打在收集板D上，在M、N间所加电压的范围为
≤U≤qB2R2 6m
；3qB2R2 2m
（3）若粒子恰好打在收集板D的中点上，粒子从s1开始运动到打在D的中点上经历的时间是
．(6+π)m 2qB
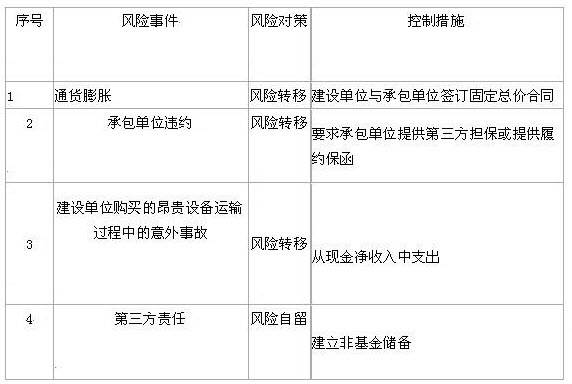乙施工单位投保了建筑工程保险和附加第三者责任险。在施工过程中；对材料进行分隔存放。 建设单位向丙公司预定产品。订货合同规定了设备类型和数量，并规定了以美元作为支付货币，建设单位支付10%的定金。生产时间通常是4个月至9个月建设单位担心人民币兑美元可能贬值；决定对风险套期保值，有效地使人民币的美元价值固定，从而使设备合同的美元价值固定。