如图所示,在半径为R的圆周上的六个等分点分别为C、D、E、F、G、H,其中以D、E、G、H为圆心、R/4为半径的圆形区域有垂直纸面向里磁感应强度为B0的匀强磁场,在圆周两侧关于O对称的位置有两单边界匀强磁场.其边界与HG所在直线垂直.一个质量为m电荷量为+q的离子(不计重力),由A点(A为HG的中点)沿AH飞进小圆形磁场,之后沿HC方向飞出.离子在几个磁场中飞进飞出做周期性运动,经历一个周期再次沿AH方向通过A点.
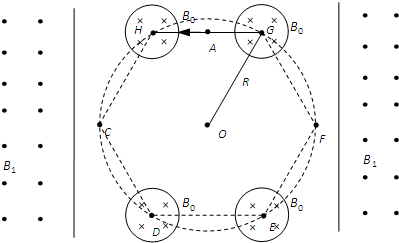
(1)求离子速度v0的大小?
(2)为使离子在两侧磁场区做圆周运动的半径为
R/2,磁感应强度B1的大小?两磁场边界的距离d为多少?3
(3)在(2)问的条件下,离子完成一次周期性运动的时间T是多少?
根据题意,粒子运动的轨迹(部分)如图:
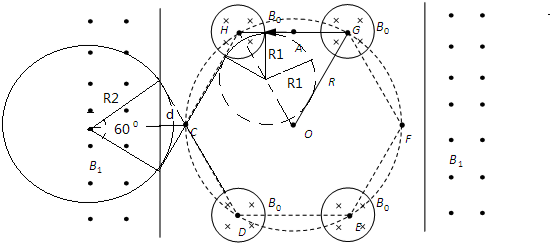
(1)在B0 的磁场区域内,粒子的偏转角为60°,其偏转半径R1 为:R1=
=R 4 tan300
R3 4
该区域内,洛伦兹力提供向心力:qvoB0=m v 20 R1
故:v0=
=qB0R1 m
qB0R3 4m
(2)在B1 的磁场区域内,粒子的偏转角为3000,如图,洛伦兹力提供向心力:qvoB1=m v 20 R2
故:B1=B0 2
由图可得边界到C点的距离:d′=R2sin300?sin300=
R3 8
两磁场边界的距离d为:d=2R+2d′=(2+
)R3 2
(3)粒子在B0 的磁场区域内的周期:T1=2πm qB0
粒子在B0 的磁场区域内的时间:t1=
T1=θ 2π πm 3
粒子在B1 的磁场区域内的周期:T2=
=2πm qB1 4πm 3qB0
粒子在B1 的磁场区域内的时间:t2=
T2=θ′ 2π 10πm 3qB0
粒子在两个磁场之间做匀速直线运动,距离:L=
R+R2Sin300=3 4
R3+ 3 4
粒子在两个磁场之间的运动时间:t3=
=L v0 (1+
)m3 qB0
D到E和F到G之间的没有磁场的区域时间均为:t4=
=R 2v0
m3 3qB0
粒子运动的总时间:t总=4t1+2t2+4t3+2t4=24πm+12m+14
m3 3qB0
答:(1)粒子的速度为:
;(2)B1=
qB0R3 4m
;两磁场边界的距离d为:(2+B0 2
)R;(3)粒子运动的总时间:3 2 24πm+12m+14
m3 3qB0
